Pythonでコッホ曲線を描く

土曜日なので，コッホ曲線を描いて遊んでみた．

コッホ曲線とは，

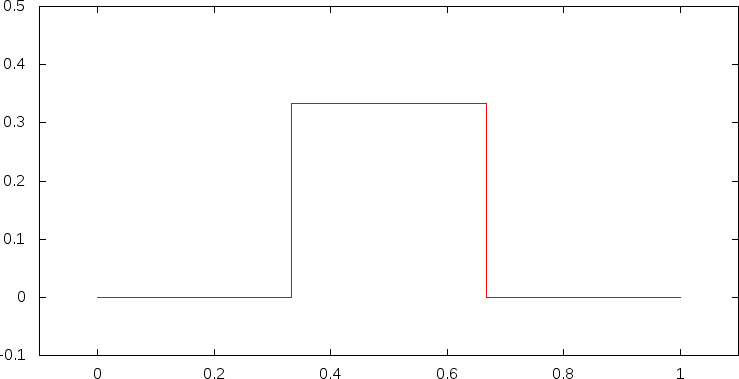
こんな感じのパターンを定義して，パターンの各線分をパターンで置き換える，というのを再帰的に繰り返してできるフラクタル図形．
一度置き換えると，こんな感じ．

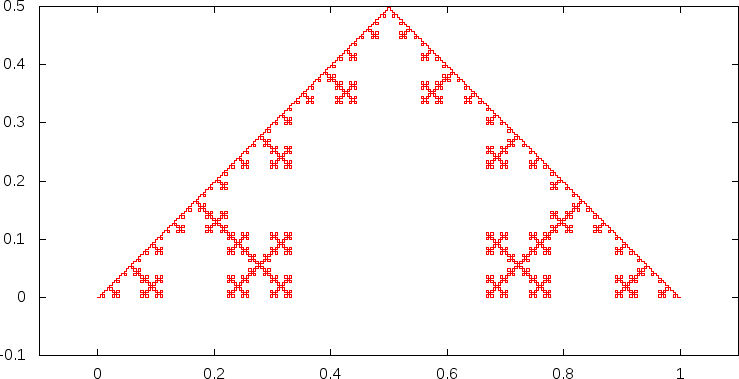
5回で，

となる．

パターンを

これに置き換えると，

こんな感じになる．

プログラムはPythonで作って，Gnuplotで描画した．

#!/usr/bin/python
from numpy import *
from math import *

def Rot(p,theta):
  c= cos(theta)
  s= sin(theta)
  p2= array([p[0]*c-p[1]*s, p[0]*s+p[1]*c])
  return p2

def DrawLineRecursively(x1,x2,p_list,n,N):
  if n==N:
    print ' '.join(map(str,x1))
    print ' '.join(map(str,x2))
  else:
    p0= p_list[0]
    d1= p_list[-1]-p_list[0]
    d2= x2-x1
    f= linalg.norm(d2)/linalg.norm(d1)
    d= x1-p0
    theta= acos(dot(d1,d2)/(linalg.norm(d1)*linalg.norm(d2)))
    if cross(d1,d2)<0: theta=-theta
    pa= p_list[0]
    for pb in p_list[1:]:
      pa2= f*Rot(pa-p0,theta)+d
      pb2= f*Rot(pb-p0,theta)+d
      DrawLineRecursively(pa2,pb2,p_list,n+1,N)
      pa= pb

こんな感じで関数を用意して（かなり雑に書いたorz；パターンの回転，平行移動，リサイズを適当に繰り返してるだけ），

p_list= array([[0,0],[1,0],[1.5,sqrt(3)/2.0],[2,0],[3,0]])
DrawLineRecursively(array([0,0]),array([1,0]),p_list,0,5)

みたいに使う．引数の最後の5は，再帰の深さ．

パターンは p_list で定義している．パターンを変えて遊んでみよう．
これは前出のやつ：

p_list= array([[0,0],[1,0],[1,1],[2,1],[2,0],[3,0]])

いろいろ試す：

p_list= array([[0,0],[1,0],[1,1],[2,1],[2,-1],[3,-1],[3,0],[4,0]])

p_list= array([[0,0],[1,0],[1,2],[2,2],[2,0],[3,0]])

p_list= array([[0,0],[1,0],[1.5,2],[2,0],[3,0]])

多角形の各辺にコッホ曲線をのせて描くのも面白い．

p_list= array([[0,0],[1,0],[1.5,sqrt(3)/2.0],[2,0],[3,0]])
NN=6
for i in range(0,NN):
  p1= Rot(array([0,1]),2.0*pi/float(NN)*i)
  p2= Rot(array([0,1]),2.0*pi/float(NN)*(i+1))
  DrawLineRecursively(p1,p2,p_list,0,4)

p_list= array([[0,0],[1,0],[1,1],[2,1],[2,0],[3,0]])
NN=8

真面目な知識はWikiで．英語版のウィキペディアが面白い．

• Koch snowflake

初めてコッホ曲線を描いたのは中学のときで，そのときは本を見て描いたのだけど，数学の自由研究の課題（？）で提出したら市か何かの佳作か努力賞か何かの賞をもらった（ずいぶん記憶が曖昧に．．．）．